The Mayan Numbers uses a 20 base system, called the vigesimal number system. Just as our own ten based numeric system was probably used because we have 10 fingers on our hands, the Mayan numeric system was probably based on the number of fingers on both the hands and feet.
The Mayans used the numbers to make surprisingly accurate measurements in their Calendrical System and the construction of incredible buildings such as the Kukulkán pyramid in Chichén Itzá, The Pyramid of the Magician in Uxmal, among others.
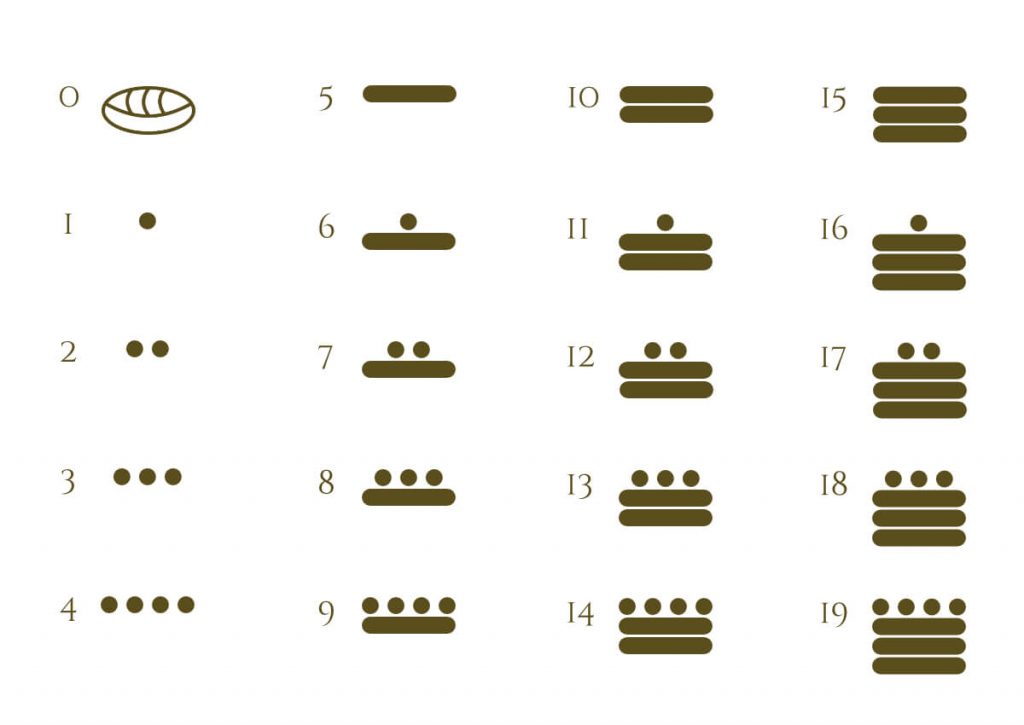
The representation of the Mayan Numbers

The ancient Mayans could express any number from zero to infinity using only 3 symbols, the shell, a dot, and a horizontal line.
The shell has a value of 0, the dot is worth 1 and the line is worth 5.
An interesting fact is that the Mayan system may have been the first to make use of zero as a placeholder, and as a number in the entire known human history.
Positional system
Just like our system, the Mayan numbers are also positional, which means that the position of a numeric symbol indicates its value. With this they could represent incredibly large numbers just by positioning them vertically, adding the multiple of 20 in the position above.
Unlike our system, where the unit’s position starts on the right and then moves to the left to represent a higher value, the Mayan system starts at the bottom and the units are added upwards as it increases its positional value.
How the Mayan Numbers work
As we have seen, there are only 3 symbols with which we can represent any number based on the vertical position, the higher they are, the more value they represent.
When writing the Mayan Numbers, the number of dots is limited to 4 and the number of bars is limited to 3. So, if we want to represent the number 5, we can NOT use 5 dots, instead, we can add a bar that represents that amount.
The first position
In the first position, we can only represent up to number 19.
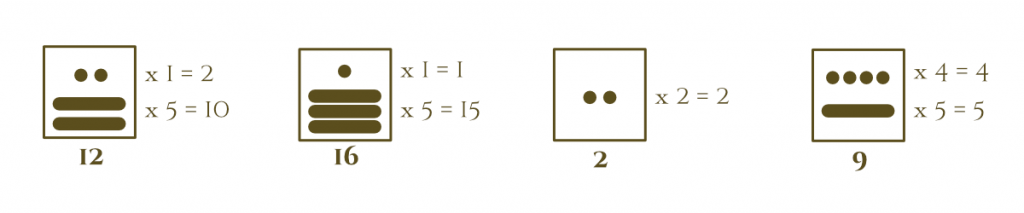
There should never be more than four dots and three bars.
Second position
By putting a value in the second position, it’s raised to the twentieth power; in other words, it’s multiplied by 20.
The dots and lines in the first position keep their original value, but those in the second position get multiplied by 20.
If we have a dot in the second position, instead of having a value of 1, it’s now worth 20 (1×20).
The bar instead of having a value of 5, is now worth 100 (5×20).
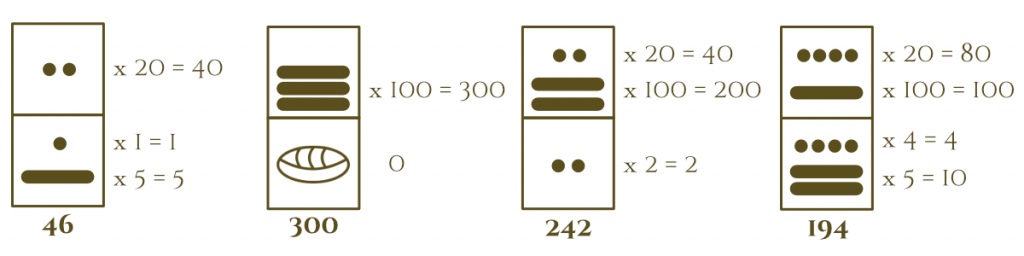
If you want to represent the number 20, you have to put the Shell (worth zero) in the first position, the same if you want to represent any other multiple of 20 such as 40, 60, 100, 200, etc.
More positions for Mayan numbers
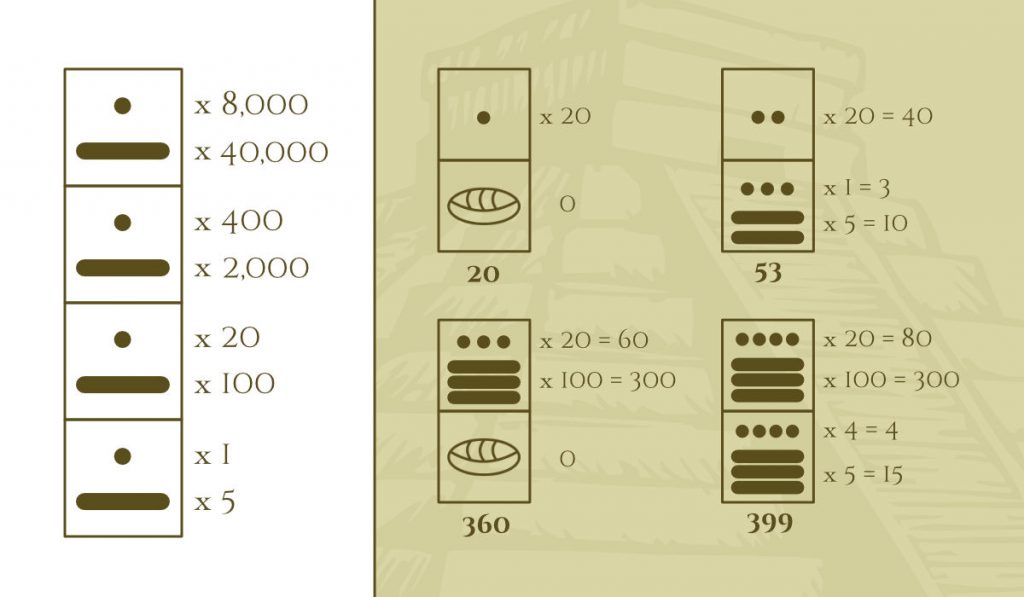
Just as we saw in the first and second positions, and how they acquire a different value depending on where they are, we can continue adding more positions to represent increasing numerical values.
The numbers in the Mayan Language
| 1 | jun | 11 | jun lajun |
| 2 | ka’a | 12 | ka’a lajun |
| 3 | óox | 13 | óoxlajun |
| 4 | kan | 14 | kanlajun |
| 5 | jo’o | 15 | jo’olajun |
| 6 | waak | 16 | waaklajun |
| 7 | u’uk | 17 | u’uklajun |
| 8 | waxak | 18 | waxaklajun |
| 9 | bolon | 19 | bolonlajun |
| 10 | lajun | 20 | jun k’aal |
| 200 | 1 | Jun |
| 201 | 20 | Jun k’aal |
| 202 | 400 | Bak |
| 203 | 8,000 | Pic |
| 204 | 160,000 | Kabal |
| 205 | 3,200,000 | Kinchil |
| 206 | 64,000,000 | Alau |
| 207 | 12,800,000,000 | Hablat |
Other numbering systems
There were two numbering systems developed by the Mayans: one for ordinary people and one for priests. These two systems not only used different symbols, but also used different base systems.
For priests, the number system was governed by ritual and the days of the year were thought to be gods, so the formal symbols for the days were decorated heads.
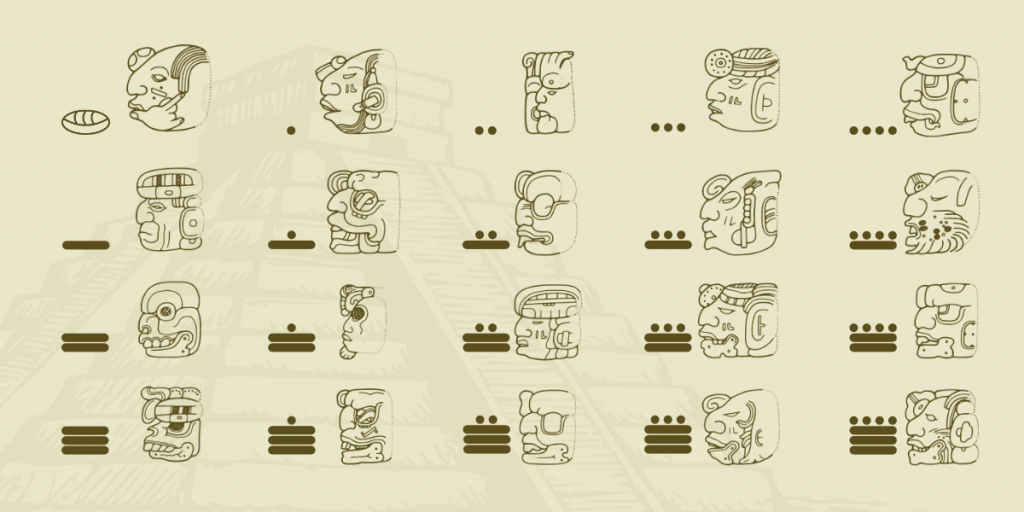
Interactive exercise with Mayan Numbers
Now that you have learned the numbers in the Mayan Language, I invite you to do the following interactive exercise so that you can test yourself:











